Встроенные специальные математические функции
Наряду с элементарными функциями в системе MathCAD содержится ряд встроенных специальных математических функций. Их применение расширяет возможности системы в решении сложных математических задач.
Функции Бесселя
К важнейшим встроенным специальным математическим функциям принадлежат функции Бесселя, являющиеся решениями дифференциального уравнения второго порядка:
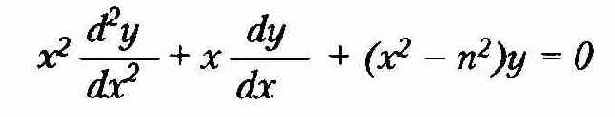
Здесь п — порядок функции (рассматриваются функции только целого порядка при действительном х). Функции Бесселя описывают колебательные процессы и широко используются в физике и электро- и радиотехнике. Приведенное уравнение имеет решения в виде функций Бесселя Jn(x) первого рода и Yn(:c) второго рода.
Существуют также модифицированные функции Бесселя, которые являются решениями следующего дифференциального уравнения:
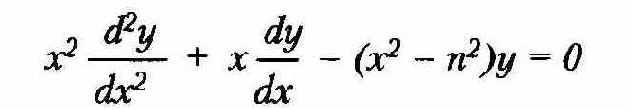
Эти функции также представлены функциями первого рода 1п(x) и второго рода Кп(х).
Функции Бесселя используются с вещественным аргументом. Ниже приведен список функций Бесселя, вычисление которых реализовано в системе MathCAD:
j0(х) —
функция Бесселя первого рода нулевого порядка;
I0(х) —
модифицированная функция Бесселя первого рода нулевого порядка;
Y0(x) — функция Бесселя второго рода нулевого порядка;
К0(х) — модифицированная функция Бесселя второго рода нулевого порядка;
J1(x) — функция Бесселя первого рода первого порядка;
I1(x) —
модифицированная функция Бесселя первого рода первого порядка;
Y1(x) — функция Бесселя второго рода первого порядка;
К1(х) — модифицированная функция Бесселя второго рода первого порядка;
Jn(n,x) — функция Бесселя первого рода п-го порядка;
1п(п,к) —
модифицированная функция Бесселя первого рода п-го порядка;
Yn(n,c) — функция Бесселя второго рода п-го порядка;
Кп(n,x) — модифицированная функция Бесселя второго рода п-го порядка.
Гамма-функция
Другой широко распространенной специальной функцией, вычисление которой (причем как при действительном, так и комплексном аргументе z)
предусмотрено в системе MahCAD, является гамма-функция G(z). Она широко применяется и в статистических расчетах. В них используется также функция ошибок erf(x), называемая еще интегралом вероятности.
На рис. 11. 9 представлены примеры вычисления ряда специальных математических функций и их графики.
Рис.11.9 Вычисление специальных математических функций
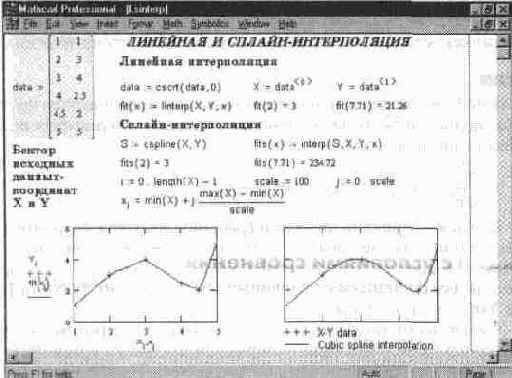
Наличие встроенных в систему наиболее распространенных математических функций расширяет ее возможности. Многие другие специальные математические функции могут быть определены через перечисленные встроенные функции или заданы своим интегральным либо дифференциальным представлением.
Дополнительные неактивные функции
При загрузке символьного процессора система распознает ряд дополнительных специальных функций, например:
FresnelC(x) — интеграл Френеля С(х);
FresnelS(x) — интеграл Френеля S(x);
Ci(x) — интегральный косинус;
Si(x) — интегральный синус;
Ег(х) — интегральная показательная функция;
dilog(x) — дилогарифм;
erf(z) — интеграл ошибок для комплексного аргумент z;
Psi(x) := , In(Go(x)) — "пси"-функция;
Psi(n,x) — п-я производная "пси"-функции.
К сожалению, статус этих функций необычен, они могут фигурировать в результатах символьных операций, но недоступны для обычных операций. Эти функции не обладают свойством эволюции, т. е. они не активны. Например, невозможно вычислить значения функций при подстановке в них числового значения аргумента и применении знака = для вывода результата вычислений. Однако, используя известные (в основном интегральные) представления для этих функций, их можно определить как функции пользователя. Выражения с неактивными функциями MathCAD размещает в буфере обмена, и их можно извлечь оттуда для обозрения.
Здесь не приводятся представления для этих функций, поскольку их легко найти в справочной системе помощи MathCAD либо в литературе, например в [14, 21]. В связи с особым статусом данного класса функций их имена не выделены жирным шрифтом.