Реализация итерационных вычислений с помощью функции until
Рекуррентное вычисление чисел Фибоначчи
Система MathCAD позволяет реализовать итерационные вычисления, обычно осуществляемые по рекуррентным выражениям. Это такие выражения, при которых значение некоторой функции ищется по одному или нескольким предшествующим ее значениям. Классическим примером рекуррентных вычислений является создание чисел Фибоначчи. Как известно, два первых числа Фибоначчи определены как 1, а последующие есть сумма двух предыдущих.
Рис. 11.35 иллюстрирует подготовку вектора, содержащего десять чисел Фибоначчи. Этот пример соответствует вычислениям по рекуррентной формуле заданное число раз.
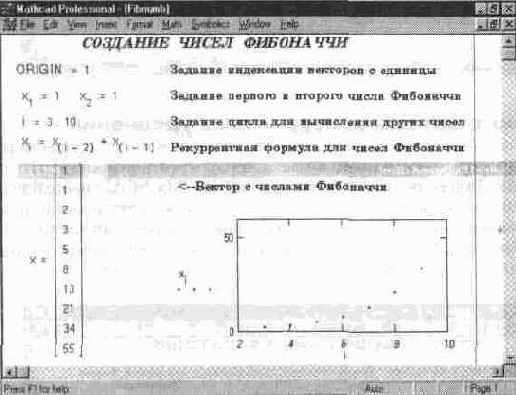
Рис. 11.35 Вычисление десяти чисел Фибоначчи
Функция until и ее применение
Более актуальна задача реализации итерационных вычислений с их окончанием по некоторому заданному условию. Для этого система MathCAD содержит специальную операцию
until(Выражение_1, Выражение_2)
Эта операция-функция реализует итерационные вычисления и возвращает значение выражения 2, если выражение 1 больше или равно 0. В противном случае итерационные вычисления прекращаются.
На рис. 11.36 показано действие этой функции на другом классическом примере — вычислении квадратного корня из числа N
итерационным методом Ньютона.
Этот пример позволяет наглядно проследить динамику схождения к точному результату результатов вычислений по итерационной формуле Ньютона.
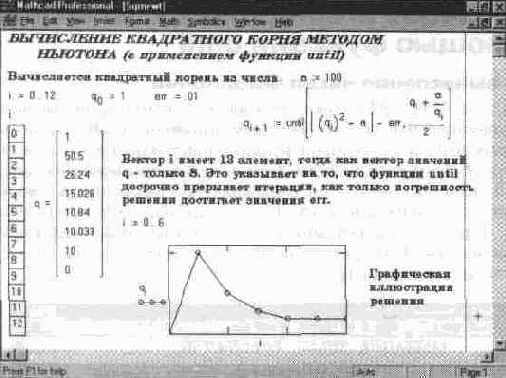
Рис. 11.36 Вычисление квадратного корня итерационным методом Ньютона
Пример решения системы рекуррентных уравнений
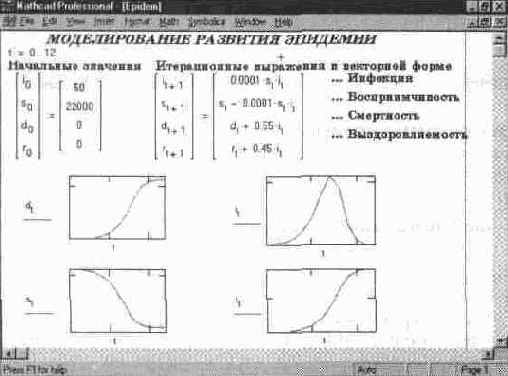
В общем случае итерационные вычисления могут осуществляться по нескольким формулам, причем возможно перекрестное применение в них переменных. Такого рода вычисления в системе MathCAD необходимо выполнять в векторной форме. Рис. 11.37 показывает решение подобной задачи — вычисляются параметры, характеризующие развитие эпидемии. По существу, здесь конечно-разностным методом решается система дифференциальных уравнений, описывающих развитие и угасание эпидемии.
Рис. 11.37 Динамика протекания процесса эпидемии
Возможны и более сложные реализации итерационных вычислений. Например, к ним сводится решение систем дифференциальных уравнений численными методами Эйлера, Рунге — Кутта и др.