Функции для проведения регрессии
Функции для линейной регрессии
Другой широко распространенной задачей обработки данных является представление их совокупности некоторой функцией у(х). Задача регрессии заключается в получении параметров этой функции такими, чтобы функция приближала облако исходных точек (заданных векторами VX и VY) с наименьшей среднеквадратичной погрешностью. Чаще всего используется линейная регрессия, при которой функция у(х) имеет вид
у(х) =а+ Ь*х
и описывает отрезок прямой. К линейной регрессии можно свести многие виды нелинейной регрессии при двупараметрических зависимостях у(х).
Для проведения линейной регрессии в систему встроен ряд приведенных ниже функций:
corr(VX, VY) — возвращает скаляр — коэффициент корреляции Пирсона;
intercrpt(VX, VY) — возвращает значение параметра а (смещение линии регрессии по вертикали);
slope(VX, VY) — возвращает значение параметра b (наклона линии регрессии).
На рис. 11.23 показан пример проведения линейной регрессии для данных, представленных значениями элементов в векторах VX и VY.
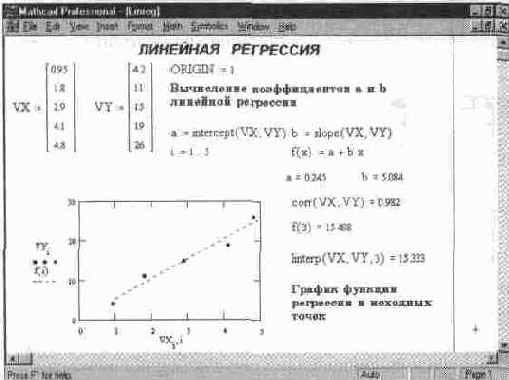
Рис.11.23 Линейная регрессия
Как видно на рис 11 23, прямая регрессии проходит в «облаке» исходных точек с максимальным среднеквадратичным приближением к ним Чем ближе коэффициент корреляции к 1, тем точнее представленная исходными точками зависимость приближается к линейной
Функция для линейной регрессии общего вида
В MathCAD реализована возможность выполнения линейной регрессии общего вида При ней заданная совокупность точек приближается функцией вида
F(x, К1 ,К2, ., Kn)= K1, F1(x)+K2 F2(x)+ +КnFn(x)
Таким образом, функция регрессии является линейной комбинацией функций F1(x), F2(x), ., Fn(x), причем сами эти функции могут быть нелинейными, что резко расширяет возможности такой аппроксимации и распространяет ее на нелинейные функции
Для реализации линейной регрессии общего вида используется функция linfit(VX,VY,F)
Эта функция возвращает вектор коэффициентов линейной регрессии общего вида К, при котором среднеквадратичная погрешность приближения облака исходных точек, если их координаты хранятся в векторах VX и VY, оказывается минимальной Вектор F должен содержать функции F1(x), F2(x), , Fn(x), записанные в символьном виде
Рис 11 24 поясняет проведение линейной регрессии общего вида с применением функции Unfit Процедура проведения вычислений настолько проста, что не нуждается в особых комментариях
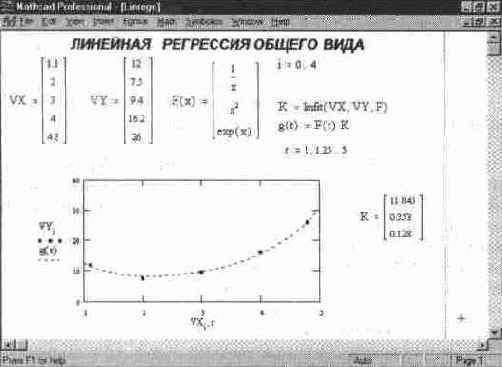
Рис. 11.24 Пример проведения линейной регрессии общего вида
Расположение координат точек исходного массива может быть любым, но вектор VX должен содержать координаты, упорядоченные в порядке их возрастания, а вектор VY ординаты, соответствующие абсциссам в векторе VX
Функции для одномерной и многомерной полиномиальной регрессии
Введена в новую версию MathCAD и функция для обеспечения полиномиальной регрессии при произвольной степени полинома регрессии
regress(VX,VY, n)
Она возвращает вектор VS, запрашиваемый функцией interp(VS,VX,VY,x), содержащий коэффициенты многочлена п-й степени, который наилучшим образом приближает «облако» точек с координатами, хранящимися в векторах VX и VY
На рис 11 25 показан пример выполнения полиномиальной регрессии Для вычисления коэффициентов полинома регрессии используется функция submatrix
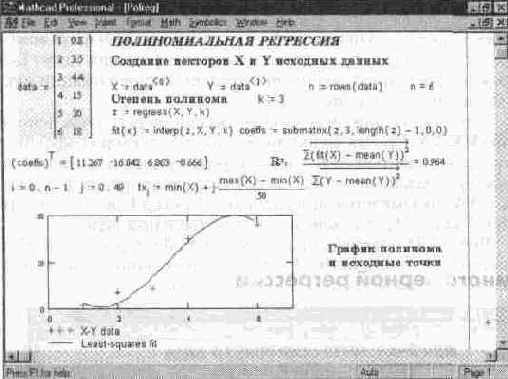
Рис. 11.25 Полиномиальная регрессия
На практике не рекомендуется делать степень аппроксимирующего поли нома выше четвертой — шестой, поскольку погрешности реализации регрессии сильно возрастают
Функция regress создает единственный приближающий полином, коэффициенты которого вычисляются по всей совокупности заданных точек, т е глобально Иногда полезна другая функция полиномиальной регрессии, дающая локальные приближения отрезками полиномов второй степени, — loess(VX, VY, span). Эта функция возвращает используемый функцией interp(VS,VX,VY,x)
вектор VS, дающий наилучшее приближение данных (с координатами точек в векторах VX и VY) отрезками полиномов второй степени Аргумент span>0
указывает размер локальной области приближаемых данных (рекомендуемое начальное значение — 0,75) Чем больше span, тем сильнее сказывается сглаживание данных При больших span эта функция приближается к regress(VX,VY,2)
На рис 11 26 показан пример приближения сложной функции со случайным разбросом ее ординат с помощью совокупности отрезков полиномов вто рой степени (функция loess)